Variational Autoencoder (VAE)

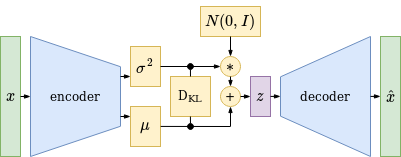Variational Autoencoder Variational Autoencoder Structure

A Variational AutoEncoder is trained like a normal autoencoder to minimize the reconstruction loss, but in addition the latent space representation of the dataset is optimized to form a gaussian normal distribution with zero mean and unit variance. This can be done by using the Kullback-Leibler Divergence that calculates the distance between two probability distributions and allows to minimize this distance by gradient descent with respect to the encoder parameters. To get a robust latent space representation, latent space vectors are sampled using a gaussian distribution and the decoder is optimized to correctly map these sampled latent space vectors to the original target vectors. This adds a stochastic element to the learning process and prevents the VAE - together with the latent space regularisation - from overfitting. As a result - after training - the decoder can be used to generate new, better interpolated and more meaningful output data from unseen latent space vectors.

Deriving the Kullback-Leibler Divergence Loss

The Kullback-Leibler Divergence between the encoder output multivariate normal distribution

\[p(z \vert x) = \mathcal{N}(z \vert \mu_x, \Sigma_x) = \mathcal{N}(\mu_0, \Sigma_0)\]

and the desired zero mean unit variance latent space normal distribution

\[p(z) = \mathcal{N}(0, \pmb{I}) = \mathcal{N}(\mu_1, \Sigma_1)\]

is defined as

\[D_{KL}(\mathcal{N}_0 \vert\vert \mathcal{N}_1) = \frac{1}{2} \left( tr(\Sigma_1^{-1}\Sigma_0) + ln \left( \frac{\vert\Sigma_1\vert}{\vert\Sigma_0\vert} \right) - n + (\mu_1 - \mu_0)^T\Sigma_1^{-1}(\mu_1 - \mu_0) \right)\]

with \(\mu_1 = 0\) and \(\Sigma_1 = \pmb{I}\) we get

\[D_{KL}(\mathcal{N}_0 \vert\vert \mathcal{N}_1) = \frac{1}{2} \left( tr(\pmb{I}^{-1}\Sigma_0) + ln \left( \frac{\vert\pmb{I}\vert}{\vert\Sigma_0\vert} \right) - n + (0 - \mu_0)^T\pmb{I}^{-1}(0 - \mu_0) \right)\] \[D_{KL}(\mathcal{N}_0 \vert\vert \mathcal{N}_1) = \frac{1}{2} \left( tr(\Sigma_0) - ln( \vert\Sigma_0\vert ) - n + \mu_0^T\mu_0 \right)\]

with i as the n-dimensional latent space feature index

\[D_{KL}(\mathcal{N}_0 \vert\vert \mathcal{N}_1) = \frac{1}{2} \left( \sum_i \sigma_i^2 - ln( \prod_i \sigma_i^2 ) - n + \sum_i \mu_i^2 \right)\]

we get the loss function based on the encoder output variance and mean vectors

\[D_{KL}(\mathcal{N}_0 \vert\vert \mathcal{N}_1) = \frac{1}{2} \left( \sum_i \sigma_i^2 - \sum_i ln( \sigma_i^2 ) - n + \sum_i \mu_i^2 \right)\] \[D_{KL}(\mathcal{N}_0 \vert\vert \mathcal{N}_1) = \frac{1}{2} \sum_i \left( \sigma_i^2 - ln( \sigma_i^2 ) - 1 + \mu_i^2 \right)\]

The derivative of the loss function with respect to \(\sigma^2\) gives us the variance gradient

\[\frac{d D_{KL}}{d \sigma_i^2} = \frac{1}{2} \left( 1 - \frac{1}{\sigma_i^2} \right) = \frac{1}{2} - \frac{1}{2 \sigma_i^2}\]

and the derivative of the loss function with respect to \(\mu\) gives us the mean gradient

\[\frac{d D_{KL}}{d \mu_i} = \frac{1}{2} \left( 2 \mu_i \right) = \mu_i\]

Nomenclature

  • x and z : encoder input vector and latent space vector.
  • p : probability distribution.
  • \(\mathcal{N}\) : a gaussian normal distribution, represented by an expected value vector and a covariance matrix.
  • \(\pmb{I}\) : identity matrix.
  • \(\Sigma\) : the covariance matrix of a probability distribution. In case of the VAE, the latent space covariance matrix is defined as a diagonal matrix and can therefore be represented by its diagonal vector. The non-diagonal elements are supposed to be 0 which implies that the latent space features are uncorrelated / independent of each other.
  • \(\sigma^2\) : a variance vector = vector of squared standard deviation values.
  • \(\mu\) : a mean vector.
  • \(tr(A)\) : the trace of the matrix that equals the sum over all diagonal elements of the matrix.
  • \(\vert A \vert\) : the determinant of the matrix that - in case of a diagonal matrix - equals the product over all diagonal elements of the matrix.
  • \(ln\) : the natural log is a good choice when calculating the Kullback-Leibler Divergence of multivariate normal distributions.

To get meaningful variance values - which are always positive - the activation function which generates \(\sigma^2\) has to softly map negative values from the encoder network to positive values. A good choice is the Softplus activation function. This also prevents negative values to be fed into the log function which is part of the Kullback-Leibler Divergence loss. The mean vector \(\mu\) can simply be generated using a Linear activation function.

Variational Autoencoder Implementation

import numpy_neural_network as npnn
import npnn_datasets
from numpy_neural_network import Sequential

encoder_model = npnn.Sequential()
encoder_model.layers = [
  npnn.Conv2D(shape_in=(3, 3, 1), shape_out=(2, 2, 6), kernel_size=2, stride=1),
  npnn.Tanh(2 * 2 * 6),
  npnn.Conv2D(shape_in=(2, 2, 6), shape_out=(1, 1, 2), kernel_size=2, stride=1),
  npnn.Tanh(1 * 1 * 2),
  npnn.Latent(shape_in=(1, 1, 2))
]

decoder_steps_per_encoder_step = 25

class DecoderSequential(Sequential):

  # override of Sequential step method
  def step(self, x=None, t=None):
    global decoder_steps_per_encoder_step

    g_dec = np.zeros(x.shape)

    for _ in np.arange(decoder_steps_per_encoder_step):
      x_dec = x.copy()
      t_dec = t.copy()

      x_dec = self.forward(x_dec)
      g, y_dec = self.chain.step(x=x_dec, t=t_dec)
      g_dec += self.backward(g)

    g_dec         = g_dec               / decoder_steps_per_encoder_step
    self.loss     = self.chain.loss     / decoder_steps_per_encoder_step
    self.accuracy = self.chain.accuracy / decoder_steps_per_encoder_step
    return g_dec, y_dec

decoder_model = DecoderSequential()
decoder_model.layers = [
  npnn.Sample(shape_out=(1, 1, 2)),
  npnn.UpConv2D(shape_in=(1, 1, 2), shape_out=(2, 2, 6), kernel_size=2, stride=1),
  npnn.Tanh(2 * 2 * 6),
  npnn.UpConv2D(shape_in=(2, 2, 6), shape_out=(3, 3, 1), kernel_size=2, stride=1),
  npnn.Tanh(3 * 3 * 1),
  npnn.Dense(shape_in=(3, 3, 1), shape_out=(3, 3, 1)),
  npnn.Linear(3 * 3 * 1)
]

kl_loss_layer = npnn.loss_layer.KullbackLeiblerLoss(shape_in=(1, 1, 4))
loss_layer    = npnn.loss_layer.RMSLoss(shape_in=(3, 3, 1))
optimizer     = npnn.optimizer.Adam(alpha=5e-3)
dataset       = npnn_datasets.FourSmallImages()

encoder_model.chain = kl_loss_layer
kl_loss_layer.chain = decoder_model
decoder_model.chain = loss_layer

optimizer.norm  = dataset.norm
optimizer.model = encoder_model

Variational Autoencoder with Latent Space Regularisation using KL-Divergence

Variational Autoencoder References

Deep Generative Modeling, MIT 6.S191 Ava Soleimany - Deep Generative Modeling, MIT 6.S191 (2020)

Generative Models, Stanford University cs231n Serena Yeung - Generative Models, Stanford University cs231n (2017)